1534: 哪个厂家的零件更标准
内存限制:128 MB
时间限制:1.000 S
标准输入输出
题目类型:传统
评测方式:文本比较
上传者:
提交:3
通过:3
题目描述
在统计描述中,方差用来计算每一个变量(观察值)与总体均数之间的差异。比如:甲乙 2 个厂商生产某零件,一批零件要求在尺寸合格的情况下,大小越一致越好,由于生产工艺的问题,零件生产厂商生产的零件不可能一模一样。
为了检测甲乙两个厂商,哪个厂商生产的零件更符合标准,分别从 2 个厂商生产的零件中抽取 5 个样品尺寸如下:
甲:100 101 102 100 99;
乙:98 100 105 103 96;
假设零件尺寸在 95∼110 之间都算合格,那么两批零件都是合格的;如果按照平均数计算,两组数据的平均值都是 100.4。
但如果将两组数据画到数轴上:
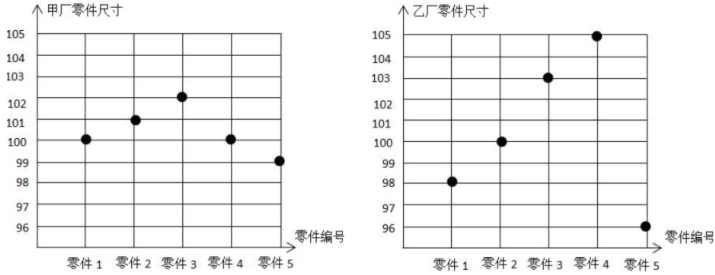
为了检测甲乙两个厂商,哪个厂商生产的零件更符合标准,分别从 2 个厂商生产的零件中抽取 5 个样品尺寸如下:
甲:100 101 102 100 99;
乙:98 100 105 103 96;
假设零件尺寸在 95∼110 之间都算合格,那么两批零件都是合格的;如果按照平均数计算,两组数据的平均值都是 100.4。
但如果将两组数据画到数轴上:

从两个厂抽检的零件分布图可以看出,甲厂的零件大小更加一致,更加符合标准。
为了方便计算数据的离散程度,我们引入方差的概念,方差的计算公式为:s2=[(x1−x)2+(x2−x)2+⋯+(xn−x)2]
其中 x1∼xn 代表一组数据中的每个元素, x 代表这组数据的平均值。
按照公式,甲厂零件的方差为:(100−100.4)2+(101−100.4)2+(102−100.4)2+(100−100.4)2+(99−100.4)2=5.2
乙厂零件的方差为:(98−100.4)2+(100−100.4)2+(105−100.4)2+(103−100.4)2+(96−100.4)2=53.2
从方差上也可以看出,甲厂的零件更符合标准!
现从键盘读入 2 个厂生产的零件尺寸(假设零件的尺寸都是合格的),请计算哪个厂的零件尺寸更加一致(方差更小)?
输入格式
第一行为一个整数 n,代表 2 个厂抽检的零件的个数!( n 在 5∼100 之间);
第二行为 n 个整数,代表甲厂的 n 个零件的尺寸;
第三行为 n 个整数,代表乙厂的 n 个零件的尺寸。
所有零件的尺寸都在 1∼1000 的范围内。
第二行为 n 个整数,代表甲厂的 n 个零件的尺寸;
第三行为 n 个整数,代表乙厂的 n 个零件的尺寸。
所有零件的尺寸都在 1∼1000 的范围内。
输出格式
哪个厂的零件更加符合标准,甲厂请输出“jia”,乙厂请输出“yi”。
输入样例 复制
5
100 101 102 100 99
98 100 105 103 96输出样例 复制
jia